Hardening soil
Hardening soil model představený Schanzem et al. [1] je vhodný pro modelování komplexního chování široké škály jemnozrnných zemin. Model kombinuje dva mechanismy zpevnění. Smykový mechanismus řídí vývoj plastických přetvoření způsobený deviatorickými složkami napětí. Naproti tomu tlakový mechanismus se aktivuje primárně při tlakovém módu zatížení pozorovaného např. v edometru nebo při izotropní kompresi. Projevem smykového mechanismu zpevnění je postupný vývoj smykové plochy plasticity fsHS v závislosti na aktuální hodnotě ekvivalentního deviatorického plastického převoření κs(nebo γps).
Tento proces zpevňování (expanze plochy plasticity) spojený s vývojem mobilizovaného úhlu vnitřního tření φm je ukončen dosažením limitní smykové plochy plasticity fsMN. V programu GEO5 MKP je tato plocha definovaná Matsuoka-Nakai podmínkou porušení, jež je funkcí vrcholových parametrů smykové pevnosti, koheze c a úhlu vnitřního tření φ. Průmět plochy plasticity do deviatorické roviny je tudíž hladká konvexní křivka procházející vrcholy Mohr-Coulombova modelu. Projevem tlakového zpevnění je vývoj tlakové plochy plasticity fcHS (compression cap) v závislosti na vývoji překonsolidačního napětí pc. Obdobná formulace v invariantních mírách napětí byla představena v publikaci [2].
Grafické znázornění obou ploch plasticity je patrné z následujícího obrázku. Pro ilustraci uvádíme postupný vývoj smykové plochy plasticity patrný z průmětu plochy plasticity do meridiální roviny. Podobným způsobem je definovaný Soft soil model, který ovšem zavádí pouze limitní smykovou plochu, tudíž uvažuje pouze tlakové zpevnění.
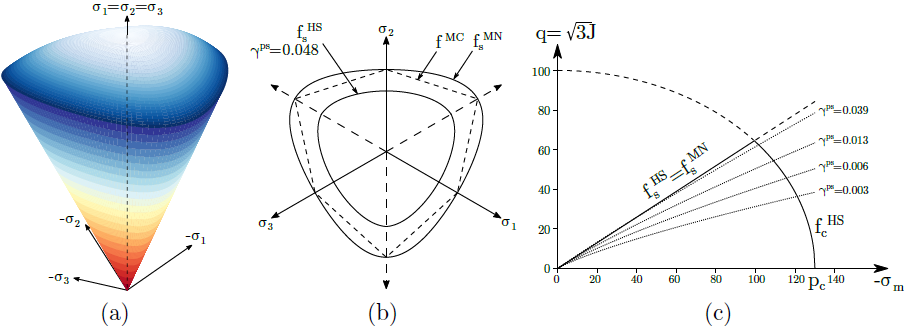 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
Formulace smykové plochy plasticity vychází z předpokladu, že vztah mezi deviatorickým napětím q a svislém přetvoření ε3 při odvodněné triaxiálové zkoušce lze popsat hyperbolickou funkcí. Příslušný pracovní diagram je vykreslen na následujícím obrázku, kde qa představuje asymptotickou hodnotu deviátoru q a qfMC odpovídá hodnotě q při dosažení limitní plochy přičemž platí qf = Rfqa, kde Rf je redukční součinitel. Další podrobnosti lze nalézt v teoretické příručce.
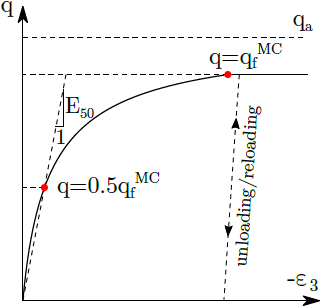 Hyperbolický pracovní diagram
Hyperbolický pracovní diagram
Parametry definující Hardening soil materiálový model jsou shrnuty v následující tabulce.
Symbol | Jednotky | Popis | |
| [MPa] | Sečný modul pružnosti | |
| [MPa] | Modul odtížení/přitížení | |
| [-] | Poissonovo číslo | |
| [kPa] | Referenční střední napětí | |
| [-] | Exponent mocninného zákona | |
| [kPa] | Limitní hodnota středního napětí pro zajištění nenulové tuhosti | |
| [kN/m3] | Objemová tíha | |
| [-] | Počáteční číslo pórovitosti odpovídající stavu na konci 1. fáze | |
| [-] | Součinitel porušení | |
| [Pa] | Vrcholová efektivní koheze | |
| [°] | Vrcholový efektivní úhel vnitřního tření | |
| [°] | Úhel dilatance | |
| [kN/m3] | Objemová tíha | |
| [-] | Součinitel příčného tlaku v klidu normálně konsolidované zeminy | |
| [MPa] | Tečný edometrický modul | |
| [kPa] | Referenční svislé napětí pro určení | |
| [-] | Maximální číslo pórovitosti pro ukončení dilatance (při omezení dilatance) | |
| [-] | Součinitel překonsolidace | |
| [Pa] | Součinitel předchozího přetížení (preoverburden pressure) | |
| [1/K] | Součinitel teplotní roztažnosti (při uvažování teploty) | |
| [-] | Parametr modelu definující tvar tlakové podmínky plasticity | |
| [kPa] | Modul zpevnění (nezadává se) | |
| [Pa] | Překonsolidační napětí | |
| [°] | Úhel vnitřního tření příslušný kritickému stavu (nezadává se) | |
| [°] | Mobilizovaný úhel vnitřního tření (nezadává se) | |
| [°] | Mobilizovaný úhel dilatance (nezadává se) |
Sečný modul pružnosti Eip,ref lze aproximovat pomocí modulu pružnosti E50p,ref následovně
![]()
kde index (p,ref) vyjadřuje referenční hodnotu modulu vztaženou k určité referenční hodnotě středního napětí σmref. Obecně model předpokládá závislost tuhosti na aktuálním středním napětí ve tvaru
![]()
Poznamenejme, že tato formulace se liší od formulace použité např. v publikacích [1] a [2], kde vývoj tuhosti je vyjádřen v závislosti na minimálním hlavním napětí, zde σ1. Toto je třeba si uvědomit při přímém použití parametrů kalibrovaných pro jiný inženýrský software v programu GEO5 MKP, což může vést k rozdílům ve výsledných predikcích. Určitou možností je použití upravených parametrů, které poskytnou rozumnou shodu výsledných simulací obou programů. V případě parametrů Eurp,ref a mp lze použít lineární regresi. Výsledek tohoto přístupu je ilustrován na následujícím obrázku.
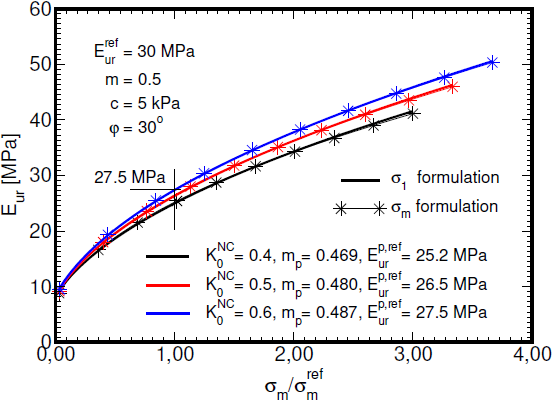 Určení závislosti modulu odtížení/přitížení Eur na středním napětí σm lineární regresí
Určení závislosti modulu odtížení/přitížení Eur na středním napětí σm lineární regresí
Upravené parametry E50p,ref(Eip,ref) a Rf lze získat následně v rámci optimalizace porovnáním numerických simulací triaxiálové kompresní zkoušky predikované oběma implementacemi při již známých hodnotách parametrů Eurp,ref a mp. Podrobnosti lze nalézt v teoretické příručce. Pokud jsou ovšem dostupná měření ze základních laboratorních zkoušek, je vhodné použít program ExCalibre přímo na kalibraci parametrů modelu implementovaného do programu GEO5 MKP.
Tlaková plocha plasticity fcHS je charakterizovaná parametrem M definující její tvar a modulem zpevnění H vyjadřující poměr přírůstku překonsolidačního napětí Δpc a objemového plastického přetvoření Δεvpl. Parametr H je definován následovně

kde Kc, Ks představují objemové moduly za předpokladu primární zatížení, respektive odtižení. Další podrobnosti lze nalézt v teoretické příručce. Program GEO5 MKP sice umožňuje parametry ![]() přímo zadat, ale je možné je též určit na základě zadaných hodnot součinitele příčného tlaku v klidu normálně konsolidované zeminy K0NC a edometrického modulu Eoedref. Tento krok je proveden programem GEO5 MKP automaticky pomocí numerické optimalizace edometrické laboratorní zkoušky. Cílem je stanovit parametry modelu M, H tak, že numericky predikovaný edometrický modul je ve shodě s modulem zadaným pro zadanou hodnotu K0NC jak je patrné z následujícího obrázku. Střední napětí σm* a ekvivalentní deviatorické napětí J* jsou vyjádřeny vztahy
přímo zadat, ale je možné je též určit na základě zadaných hodnot součinitele příčného tlaku v klidu normálně konsolidované zeminy K0NC a edometrického modulu Eoedref. Tento krok je proveden programem GEO5 MKP automaticky pomocí numerické optimalizace edometrické laboratorní zkoušky. Cílem je stanovit parametry modelu M, H tak, že numericky predikovaný edometrický modul je ve shodě s modulem zadaným pro zadanou hodnotu K0NC jak je patrné z následujícího obrázku. Střední napětí σm* a ekvivalentní deviatorické napětí J* jsou vyjádřeny vztahy
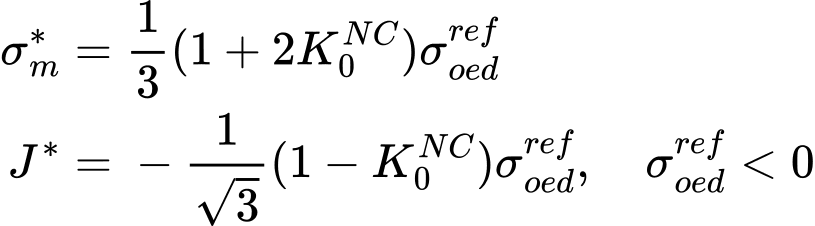
Podrobnosti lze nalézt v teoretické příručce.
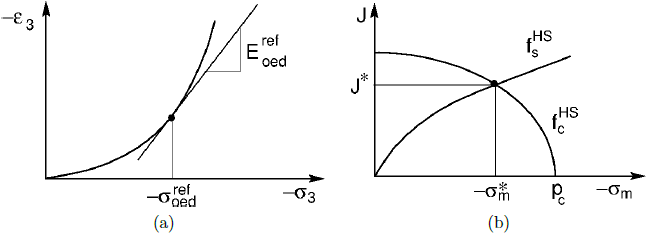 a) grafické znázornění referenčního edometrického modulu Eoedref v bodě svislého referenčního napětí σoedref, b) aktuální napětí na konci optimalizačního kroku příslušné σoedref
a) grafické znázornění referenčního edometrického modulu Eoedref v bodě svislého referenčního napětí σoedref, b) aktuální napětí na konci optimalizačního kroku příslušné σoedref
Hardening soil model umožňuje zohlednit dilatanci materiálu (vývoj kladných objemových plastických přetvoření během plastického smýkání) zavedením úhlu dilatance ψ. Vývoj plastických přetvoření je řízen tzv. plastickým potenciálem gsHS. Definice plastického potenciálu je v podstatě shodná s formulací představenou pro Drucker-Pragerův model s tím rozdílem, že směrnice plastického potenciálu Mψ závisí na aktuálním, mobilizovaném, úhlu dilatance ψm. Evoluční rovnice tohoto parametru, podobně jako v případě Modifikovaného Mohr-Coulombova modelu, vychází z Roweovy teorie dilatance
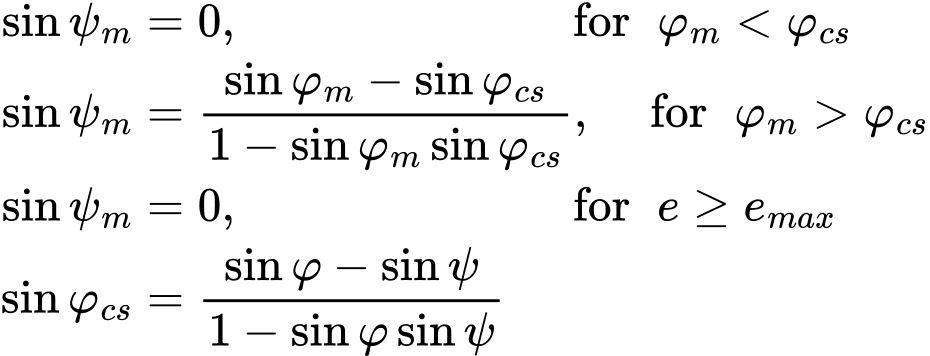
kde φ, φm, φcs, ψ jsou vrcholový úhel vnitřního tření, mobilizovaný úhel vnitřního tření, úhel vnitřního tření příslušný kritickému stavu a vrcholový úhel dilatance. Grafické znázornění vývoje ψm je patrné z následujícího obrázku. Tento obrázek také ilustruje možnost omezení dilatance zavedením maximálního čísla pórovitosti emax, pro které předpokládáme dosažení kritického stavu, tedy ψm = 0.
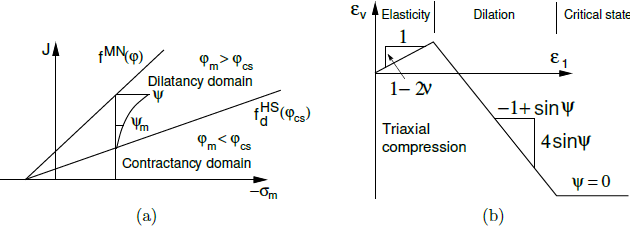 Roweova teorie dilatance: a) grafické znázornění vývoje mobilizovaného úhlu dilatance ψm, b) omezení dilatance
Roweova teorie dilatance: a) grafické znázornění vývoje mobilizovaného úhlu dilatance ψm, b) omezení dilatance
Připomeňme, že vývoj tuhosti závisí na aktuální hodnotě středního efektivního napětí σm. S tím souvisí také volba počátečního výpočtového kroku, kdy při velmi malých hodnotách napětí je nutné volit tento krok dostatečně malý. Pro urychlení konvergence je možné s výhodou využít parametr nastavení výpočtu Minimální počet iterací pro jeden výpočetní krok. Vliv počáteční délky kroku na predikovaný vývoj napětí a přetvoření je podrobně popsán zde.
Důležitý krok představuje také nastavení počátečních hodnot překonsolidačního napětí pcin a ekvivalentního plastického deviatorického přetvoření κsin. Oba tyto parametry se nastavují v závislosti na aktuální napjatosti v okamžiku zavedení modelu do výpočtu a to tak, aby aktuální stav napětí vyhovoval jak smykové, tak i tlakové podmínce plasticity. Podrobný popis je k dispozici zde. Lze konzultovat také popis Modifikovaného Cam clay modelu.
Model umožňuje upravit počáteční hodnotu parametru pc v závislosti na předpokládaném stupni překonsolidace pomocí parametrů ![]() a
a ![]() . Podrobnosti jsou uvedeny zde. Poznamenejme, že tento krok je umožněn pouze v případě, kdy počáteční napjatost je stanovena pomocí K0 procedury.
. Podrobnosti jsou uvedeny zde. Poznamenejme, že tento krok je umožněn pouze v případě, kdy počáteční napjatost je stanovena pomocí K0 procedury.
V případě výpočtu za předpokladu neodvodněných podmínek lze použít pouze variantu 1: Typ úlohy (1): výpočet v efektivních napětích (cef, φe).
Hardening soil model umožňuje řešit také úlohu stability. Tato možnost je však dostupná pouze v případě, kdy úloha stability je řešena v rámci příslušné fáze budování. Tlaková podmínka plasticity je v takovém případě vypnuta, stejně tak možnost vývoje mobilizovaného úhlu vnitřního tření. Při řešení této úlohy se tedy uplatní pouze limitní smyková plocha fsMN. Úloha je řešena postupnou redukcí vrcholových parametrů smykové pevnosti c, φ tak, jak je vysvětleno např. v popisu Drucker-Pragerova modelu.
Chování modelu v rámci jednoduchých laboratorních testů je ilustrováno zde včetně vlivu volby počátečního výpočtového kroku.
Pokud neexistují jasné experimentální důkazy pro odlišné hodnoty, měly by parametry Hardening soil modelu spadat do doporučených rozsahů uvedených v následující tabulce.
Symbol | Jednotky | Doporučené hodnoty | |
| [MPa] | (2, 70) | |
| [MPa] |
| |
| [kPa] | 100.0 | |
| [-] | (0.3, 0.9) | |
| [kPa] | 10.0 | |
| [-] | 0.9 | |
| [°] | (16.0, 42.0) | |
| [kPa] | (0.0, 50.0) | |
| [°] |
| |
| [-] | (0.5, 2.5) | |
| [-] | 0,2 | |
| [-] |
| |
| [-] |
| |
| [kPa] | 100.0 | |
| [MPa] |
|
Podrobná implementace Hardening soil modelu do programu GEO5 MKP je popsaná v teoretické příručce.
Literatura:
[1] T. Schanz, P.A. Vermeer, P.G. Bonnier, The hardening soil model: Formulation and verification, Beyond 2000 in Computational Geotechnics, Balkema, Rotterdam. 1999
[2] T. Benz, Small-Strain Stiffness of Soils and its Numerical Consequences, PhD thesis, University of Stuttgart, 2007