Hoek-Brown
Hoek-Brownův materiálový model je nejčastěji používaný model pro popis nelineárního chování horninového masivu. Podobně jako Mohr-Coulombův materiálový model je popsán třemi podmínkami porušení s průmětem do deviatorické roviny ve tvaru nepravidelného hexagonu. Na rozdíl od Mohr-Coulombova modelu je však průmět plochy plasticity fHB do meridiální roviny popsán nelineární funkcí. Grafické znázornění je patrné z obrázku. Je zřejmé, že stejně jako v případě Mohr-Coulombova modelu je Hoek-Brownova podmínka plasticity funkcí středního efektivního napětí σmeff a Lodeovu úhlu θ.
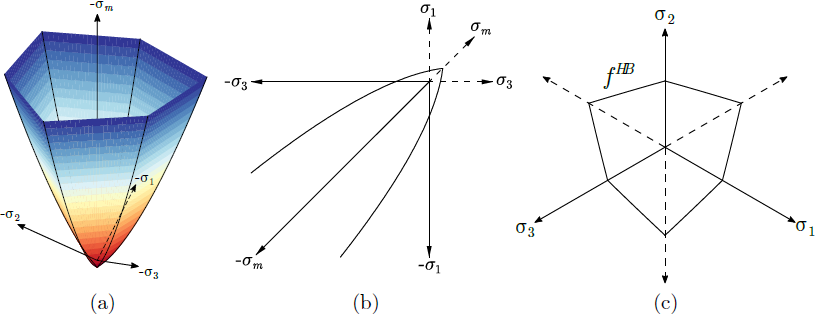 a) plocha plasticity v prostoru hlavních napětí, b) průmět do roviny maximálního a minimálního hlavního napětí c) průmět do deviatorické roviny
a) plocha plasticity v prostoru hlavních napětí, b) průmět do roviny maximálního a minimálního hlavního napětí c) průmět do deviatorické roviny
Hoek-Brownův model je čistě empirický a jeho formulace vychází z Geologického indexu pevnosti GSI (hodnota GSI =100 představuje neporušenou horninu a se stupněm porušení jeho hodnota klesá k nule), parametru rozrušení D (např. důlní činností, hodnota D = 0 odpovídá nepoškozené hornině, naopak D = 1 odpovídá hornině s maximálním stupněm poškození ), pevnosti neporušené horniny v jednoosém tlaku σci a parametru mi. Tyto dva parametry se určují z triaxiální zkoušky. Fyzikálně přípustná hodnota tahové pevnosti ![]() je
je
![]()
kde parametr s a redukovaná Hoek-Brownova konstanta mb jsou vyjádřeny pomocí parametrů GSI a D ve tvaru
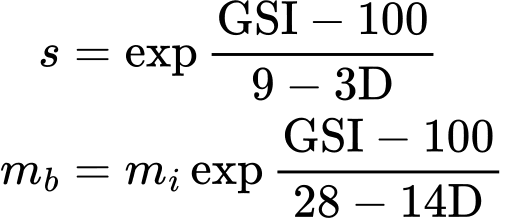
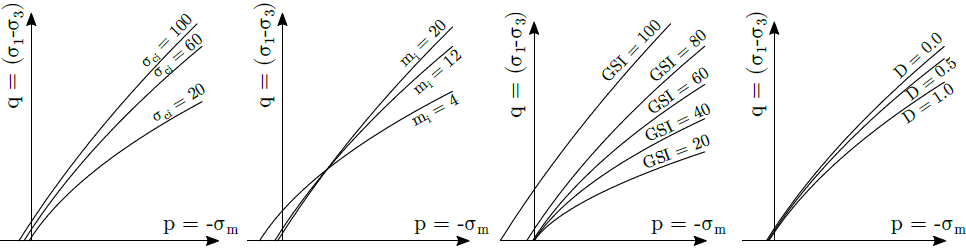
Vliv jednotlivých parametrů na průmět plochy plasticity do meridiální roviny ilustruje následující obrázek.
V případě Hoek-Brownova modelu se zadává Modul pružnosti horninového masivu Erm respektující stav porušení horniny. Lze jej stanovit např. v závislosti na parametrech modelu GSI, D a σci [2]
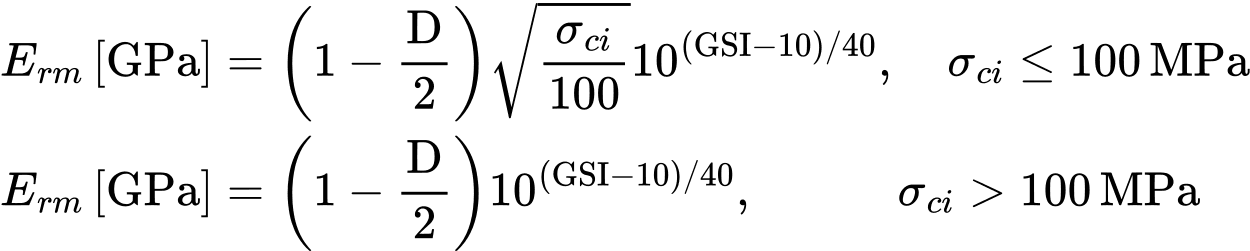
Další možnosti uvádí publikace [3].
Parametr modelu a upravující mocninný vztah v podmínce plasticity lze také vyjádřit v závislosti na geologickém indexu pevnosti GSI následovně
![]()
Parametry modelu jsou přehledně uspořádány v následující tabulce.
Symbol | Jednotky | Popis | |
| [MPa] | Modul pružnosti horninového masivu | |
| [-] | Poissonovo číslo | |
| [MPa] | Pevnost v jednoosém tlaku | |
| [-] | Hoek-Brownova konstanta | |
GSI | [-] | Geologický index pevnosti | |
D | [-] | Faktor rozrušení | |
| [°] | Úhel dilatance (zadává se počáteční hodnota | |
| [kN/m3] | Objemová tíha | |
| [-] | Redukovaná Hoek-Brownova konstanta (zadává se nebo počítá z GSI, D, | |
| [-] | Materiálová konstanta (zadává se nebo počítá z GSI, D) | |
| [kPa] | Maximální povolené tahové napětí, | |
TsRF | [-] | Součinitel redukce tahové pevnosti (0,1), pokud zadaný tak | |
| [kPa] | Limitní hodnota komorového napětí pro model dilatance | |
| [1/K] | Součinitel teplotní roztažnosti (při uvažování teploty) |
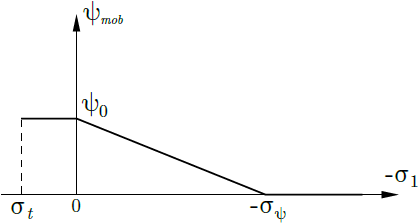
Zákon plastického tečení je podobně jako v případě Drucker-Pragerova a Mohr-Coulombova modelu obecně neasociovaný. Umožňuje tudíž zohlednit účinek dilatance materiálu (vývoj kladných objemových plastických přetvoření během plastického smýkání) zavedením úhlu dilatance ψ. Úhel dilatance však není nutně konstantní, ale může se vyvíjet podle následujícího obrázku.
Implementace Hoek-Brownova modelu automaticky zavádí hodnotu maximálního tahového napětí ![]() . Tuto hodnotu lze buď zadat nebo dopočítat na základě zadaného redukčního parametru pevnosti TsRF, viz tabulka parametrů modelu. Omezení tahové pevnosti je řízeno, podobně jako v případě Mohr-Coulombova modelu, Rankinovou podmínkou plasticity.
. Tuto hodnotu lze buď zadat nebo dopočítat na základě zadaného redukčního parametru pevnosti TsRF, viz tabulka parametrů modelu. Omezení tahové pevnosti je řízeno, podobně jako v případě Mohr-Coulombova modelu, Rankinovou podmínkou plasticity.
Model Hoek-Brown model umožňuje též řešit úlohu stability, a to jak standardní úlohu stability svahu, tak i úlohu stability řešenou v rámci dané fáze budování. Na rozdíl od modelů typu Mohr-Coulomb však zavádí parametr η redukující jednoosou tlakovou pevnost σci. Tento parametr je vyjádřen v závislosti na redukčním parametru ζ redukující standardní parametry smykové pevnosti φ, c u modelů typu Mohr-Coulomb. Stupeň stability FS je tak roven parametru ζ. Podrobnosti jsou uvedeny v teoretické příručce.
Často diskutovaná analogie s Mohr-Coulombovým modelem je podrobně popsána zde. Chování Hoek-Brownova modelu v porovnání s Mohr-Coulombovým modelem na základě jednoduchých laboratorních testů je ilustrováno v teoretické příručce.
Podrobná implementace Hoek-Brownova modelu do programu GEO5 MKP je popsaná v teoretické příručce. Další informace jsou dostupné v níže uvedených publikacích.
Literatura:
[1] E. Hoek and E.T. Brown, Practical estimates of rock mass strength, International Journal of Rock Mechanics and Mining Sciences, 34.8 (1997), 1165-1186
[2] E. Hoek, C. Carranza-Torres and B. Corkum, Hoek-Brown failure criterion - 2002 edition, Proceedings of the 5th North American symposium - NARMS-TAC (2002)
[3] E. Hoek, M.S Diederichs, Empirical estimation of rock mass modulus, International Journal of Rock Mechanics \& Mining Sciences, 43 (2006), 203-215