Mohr-Coulomb (MC)
Vzhledem k tomu, že tradiční mechanika zemin a částečně i mechanika hornin jsou založené na tomto modelu, představuje Mohr-Coulombův materiálový model jeden z nejčastěji používaných materiálových modelů v inženýrské praxi. V programu GEO5 MKP je příslušná podmínka plasticity definovaná pomocí třech mezních funkcí, jejichž zobrazením v prostoru hlavních napětích je nepravidelný šestiboký kužel. Podobně jako v případě Drucker-Pragerova modelu je podmínka plasticity závislá na středním efektivním napětí σmeff. Z průmětu plochy plasticity fMC do deviatorické roviny je zřejmé, že jednotlivé hrany se protínají v místě triaxiálové extenze θ = - 30° a triaxiálové komprese θ = 30°. Závislost podmínky plasticity na Lodeovu úhlu θ lépe odpovídá skutečnému chování zemin v porovnání s Drucker-Pragerovým modelem.
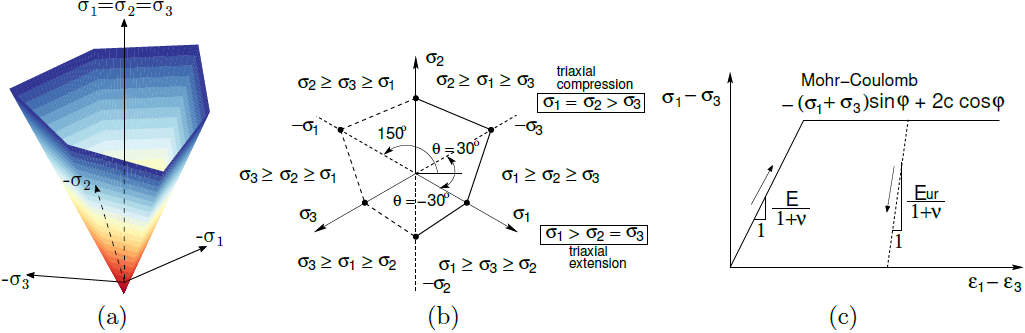 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické roviny c) pracovní diagram
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické roviny c) pracovní diagram
Z obrázku pracovního diagramu je zřejmé, že Mohr-Coulombův model umožňuje také modelovat, podobně jako Modifikovaný elastický model, rozdílné chování zeminy při primárním zatížení a odtížení a opětovném přitížení zavedením modulu odtížení/přitížení Eur.
Podobně jako Drucker-Pragerův model umožňuje Mohr-Coulombův materiálový model zohlednit vliv dilatance (vývoj kladných objemových plastických přetvoření během plastického smýkání). Obdobné je též řešení úlohy za předpokladu odvodněných a neodvodněných podmínek. Více informací včetně seznamu požadovaných materiálových parametrů lze tedy nalézt v popisu Drucker-Pragerova modelu.
Řadu ilustrativních příkladů porovnávajících skutečné a modelem predikované chování zeminy na bázi základních laboratorních testů lze nalézt zde. Příklad modelování neodvodněných podmínek je popsán zde. Podrobnější informace k implementaci odvodněných a neodvodněných podmínek lze nalézt v teoretické příručce.
Na rozdíl od Drucker-Pragerova modelu umožňuje Mohr-Coulombův model, podobně jako Hoek-Brownův model, omezit tahovou pevnost, a to buď předepsáním tahové pevnosti σt < ccotφ, kde c, φ jsou parametry smykové pevnosti zemin, anebo parametru redukce tahové pevnosti TsRF. V takovém případě platí ![]() . Numericky je omezení v tahu řízeno Rankinovou podmínkou plasticity fR. Grafické znázornění je patrné z obrázku.
. Numericky je omezení v tahu řízeno Rankinovou podmínkou plasticity fR. Grafické znázornění je patrné z obrázku.
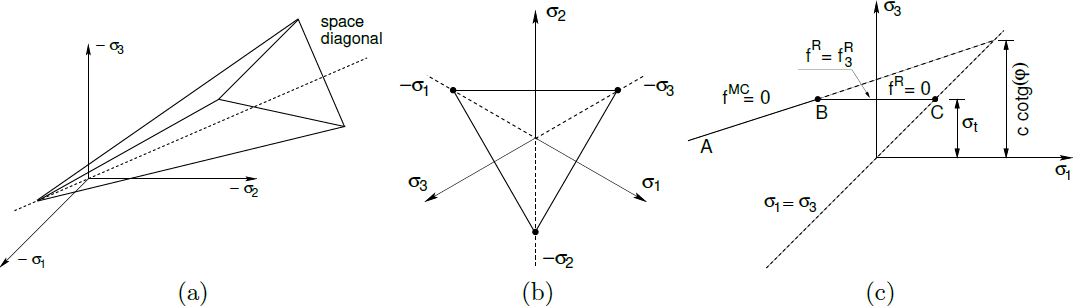 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické roviny c) průmět Mohr-Coulombovy a Rankinovy podmínky plasticity do roviny σ1 - σ3
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické roviny c) průmět Mohr-Coulombovy a Rankinovy podmínky plasticity do roviny σ1 - σ3
Mohr-Coulombův model umožňuje řešit, podobně jako Drucker-Pragerův model, úlohu stability, a to jak standardní úlohu stability svahu, tak i úlohu stability řešenou v rámci dané fáze budování. V obou případech je tato úloha řešena postupnou redukcí parametrů smykové pevnosti c, φ zavedením redukčního parametru ζ tak, že
![]()
kde c, φ jsou skutečné parametry smykové pevnosti zadané zeminy a cd, φd jsou parametry redukované. Stupeň stability FS pak určíme ze vztahu
![]()
Obdobným způsobem je redukován i úhel dilatance ψ v případě, že ψ ≠ 0.
Podrobná implementace Mohr-Coulombova modelu do programu GEO5 MKP je popsaná v teoretické příručce.