Nelineární modely
Zavedení nelineárních modelů umožňuje podstatně lépe vystihnout skutečnou odezvu zemin na účinky vnějšího zatížení. V programu GEO5 MKP jsou tyto modely formulovány buď na základě teorie plasticity anebo teorie hypoplasticity. Typickým projevem plastických modelů je vývoj trvalých plastických přetvoření umožňující grafické zobrazení potenciálních oblastí porušení např. ve formě lokalizovaného ekvivalentního deviatorického plastického přetvoření. Teorie hypoplasticity tuto možnost neposkytuje. K zobrazení očekávaných oblastí porušení lze v tomto případě využít parametr mobilizovaná smyková pevnost.
Vývoj plastických přetvoření je řízen plochou plasticity vyjadřující v prostoru napětí hranici mezi elastickou a plastickou odezvou materiálu. Matematické vyjádření plochy plasticity pak představuje určitou podmínku porušení (funkci plasticity). V případě obecné napjatosti se k vyjádření funkce plasticity většinou používají invariantní míry napětí a přetvoření. Tato funkce je buď konstantní v celém oboru zatížení (elastické-perfektně plastické materiálové modely) anebo se může měnit v závislosti na aktuálním stavu napětí a plastickém přetvoření (elasto-plastické materiálové modely se zpevněním/změkčením nebo Modely kritického stavu). Materiálový bod se v rovnovážném stavu nachází vždy uvnitř plochy plasticity (elastická odezva) anebo na ploše plasticity (plastická odezva). Další podrobnosti lze nalézt v teoretické příručce.
Jako příklad uvádíme grafické vyjádření Misesovy podmínky plasticity v prostoru hlavních napětí. Častými způsoby zobrazení jsou také průměty plochy plasticity do deviatorické a meridiální roviny, σm je střední napětí, J je ekvivalentní míra vektoru deviatorických složek napětí a θ je Lodeův úhel. Deviatorická rovina je rovina kolmá na hydrostatickou osu, pro kterou platí rovnost hlavních napětí σ1 = σ2 = σ3 = σm.
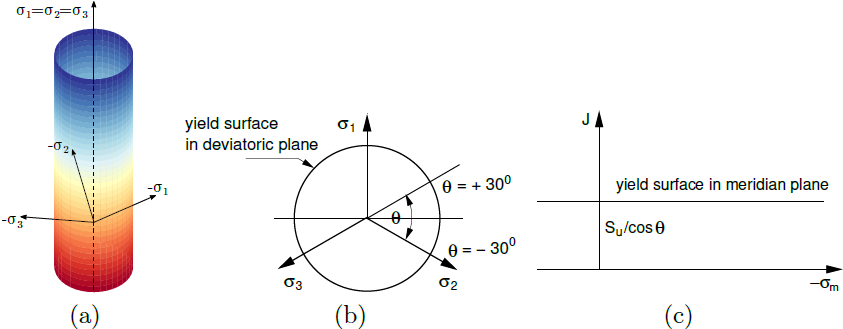 a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
a) plocha plasticity v prostoru hlavních napětí, b) průmět do deviatorické a c) meridiální roviny
- Elastické-perfektně plastické materiály. Do této skupiny materiálových modelů řadíme modely Drucker-Prager, Mohr-Coulomb, Hoek-Brown.
- Elasto-plastické materiály se zpevněním/změkčením. Do této skupiny materiálových modelů řadíme modely Hardening soil, Soft soil, Modifikovaný Mohr-Coulomb.
- Modely kritického stavu. Do této skupiny materiálových modelů řadíme modely Modifikovaný Cam-clay, Zobecněný Cam-clay, Hypoplastický jíl.
Poznámka: Na rozdíl of programu GEO5 FEM, předpokládají matematické vzorce a grafické znázornění konstitutivních vztahů a ploch plasticity a plastických potenciálů, stejně jako teoretická příručka, standardní značení teorie pružnosti, tedy tahové napětí je kladné a tlakové napětí je záporné (σ > 0 - tah, σ < 0 - tlak).