Sarma
Sarmova metoda je obecná proužková metoda mezní rovnováhy. Je založena na splnění rovnováhy sil i momentů na jednotlivých blocích. Bloky vzniknou rozdělením oblasti zeminy nad smykovou plochou rovinami, které obecně mohou mít různý sklon. Statické schéma bloků a sil, které na ně působí, je zachyceno na obrázku.
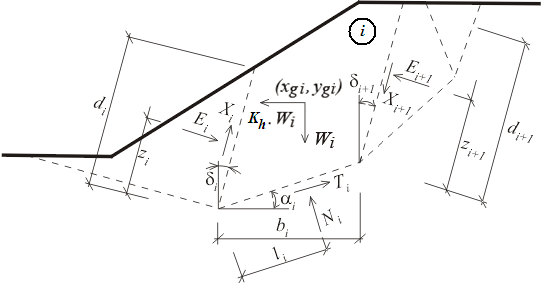 Statické schéma - Sarmova metoda
Statické schéma - Sarmova metoda
Zde Ei , Xi jsou normálové a smykové síly mezi bloky. Ni , Ti jsou normálové a smykové síly na úsecích smykové plochy. Wi je tíha bloku a Kh*Wi je vodorovná síla, pomocí níž je v Sarmově metodě dosaženo mezní rovnováhy. V každém bloku může být zadáno obecně šikmé přitížení. Toto přitížení je do výpočtu zahrnuto spolu s přitížením od vody, jejíž volná hladina je nad povrchem terénu, a se silami v kotvách. Všechny tyto síly jsou rozloženy na vodorovné a svislé složky a ty jsou pak načítány do sil FXi, FYi.
Kh je konstanta, která se nazývá faktor vodorovného zrychlení a je do výpočtu zavedena pro uvedení sil na blocích do rovnováhy. Mezi faktorem Kh a stupněm stability SF existuje závislost, pomocí níž se stupeň stability počítá. V běžném případě se stupeň stability SF počítá pro nulovou hodnotu součinitele Kh. Zavedení nenulové hodnoty faktoru Kh do výpočtu lze využít pro simulaci vodorovného zatížení terénu např. zemětřesením (viz dále).
Postup výpočtu
Výpočet limitní rovnováhy
Do výpočtu limitní rovnováhy vstupuje celkem 6n - 1 neznámých, přičemž n je počet bloků, na něž dělíme oblast nad smykovou plochou. Jsou to:
Ei | - | meziblokové síly |
Ni | - | normálové síly na smykové ploše |
Ti | - | smykové síly na smykové ploše |
Xi | - | smykové síly mezi bloky |
zi | - | polohy působišť sil |
li | - | polohy působišť sil |
Kh | - | faktor vodorovného zrychlení |
Pro jejich výpočet máme k dispozici 5n - 1 rovnic, a to:
a)vodorovné součtové výminky na blocích:
![]()
b)svislé součtové výminky na blocích:
![]()
c) momentové výminky na blocích:
![]()
kde rxi a ryi jsou ramena sil FXi a FYi
d) vztahy mezi normálovými a smykovými silami podle Mohr-Coulombovy teorie:
![]()
![]()
kde: | PWi | - | výslednice pórového tlaku na dělicích rovinách |
| - | průměrná hodnota úhlu vnitřního tření na dělicí rovině | |
| - | průměrná hodnota soudržnosti na dělicí rovině |
Je vidět, že n - 1 neznámých je třeba napřed odhadnout. Relativně malou nepřesnost způsobí odhad působišť sil Ei. Tím se problém stane staticky určitým a vyřešením soustavy rovnic lze získat hodnoty všech neznámých. Hlavním výsledkem tohoto řešení je získání faktoru vodorovného zrychlení Kh.
Výpočet stupně stability SF
Stupeň stability SF se do výpočtu zavede tak, že se jím redukují parametry zemin c a tanφ. Pro redukované parametry se znovu provede výpočet rovnováhy a tím se získá faktor vodorovného zrychlení Kh odpovídající danému stupni stability SF. Tato iterace se opakuje tak dlouho, až získaný faktor Kh dosáhne nulové hodnoty nebo hodnoty zadané.
Vliv vnějšího zatížení
Posuzovaný svah může být zatížen na povrchu šikmým zatížením obecně lichoběžníkového tvaru. Toto zatížení je do výpočtu zahrnuto tak, že jeho svislá složka, pokud má směr tíhy (hmotná složka), je přičtena k tíze toho bloku, na němž spočívá. Tím se změní jednak samotná tíha tohoto bloku a jednak poloha jeho těžiště. Pokud svislá složka působí proti směru tíhy, je přičtena k síle FYi. Vodorovná složka se přičte k síle FXi.
Literatura:
Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423-433, 1973.