Pomoc online

Argila Hipostática

A argila hipóstática é aplicada para a modelação de solos moles de graduação fina. De forma semelhante a todos os outros modelos granulares, este modelo pertence à família dos modelos fenomenológicos normais. Quanto à descrição da resposta do solo, pertence ao grupo dos modelos de estado crítico (Cam clay, Cam clay generalizado). No entanto, este modelo considera a resposta não linear dos solos, durante o carregamento e o relaxamento. Em comparação com outros modelos baseados na teoria da plasticidade, apenas é possível calcular deformações totais. Não existe diferenciamento entre deformações elásticas e plásticas. A indicação do tipo e localização da potencial rotura, que em outros modelos é dada pela definição da deformação plástica equivalente de desvio, pode ser representada pela distribuição do ângulo de atrito interno mobilizado, no caso da argila hipostática.

Ao descrever a resposta do solo, o modelo permite refletir uma rigidez diferente para o carregamento e para o relaxamento, suaviazação ou endurecimento consoante a compactação do solo e variação de volume em cisalhamento (dilatação, compressão). A rigidez depende da direção da carga, e do estado do solo dado pela sua porosidade. Ao contrário dos modelos de Cam clay, a tensão de tração do solo é estritamente excluída (ver Figura 1a).

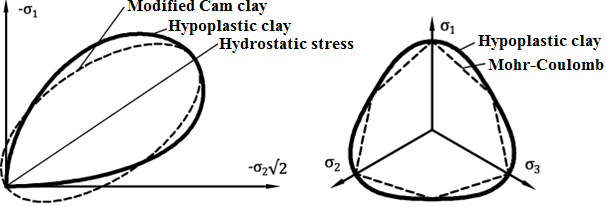Figura 1: Fronteira do estado do moldo hipoplástico - (a) comparação com a superfície de cedência do modelo de Cam clay no modelo meridiano, (b) comparação com a superfície de cedência do modelo de Mohr-Coulomb no plano de desvio

No caso do modelo hipoplástico, a superfície de cedência é substituída pela superfície de estado de fronteira. A sua projeção no plano de desvio é semelhante ao modelo (ver Figura 1b). A lei de fluxo não está associada, resultando numa matriz de rigidez assimétrica (comparar com o modelo de Mohr-Coulomb, por exemplo, quando se verificarem valores diferentes para o ângulo de atrito interno φ e para o ângulo de dilatação ψ). Podem ser encontrados detalhes acerca da formulação do modelo em [1].

Parâmetros do modelo

A variação do modelo implica a introdução de cinco parâmetros materiais:

• Ângulo de atrito interno a volume constante (ângulo de atrito interno crítico) φ_cv
• Inclinação da linha de dilatação κ*
• Inclinação da linha de consolidação normal (NCL - linha de consolidação normal) λ*
• Origem da linha de consolidação normal N
• Rácio dos módulos unitário e de cisalhamento r

Os parâmetros κ*, λ* e N determinam um diagrama bilinear de consolidação isotrópica, numa escala log-log (ver Figura 2a). Se os parâmetros do modelo bilinear de Cam clay (numa escala semi-logaritmica, Figura 2b) estiverem disponíveis, é possível introduzi-los e são utilizados pelo programa para calcular os parâmetros do modelo hipoplástico. Os parâmetros do modelo bilinear de Cam clay são:

• Inclinação da linha de dilatação κ (escala semi-logaritmica)
• Inclinação da linha de consolidação normal λ (escala semi-logaritmica)
• Índice de vazios e_max para consolidação normal isotrópica com pressão de 1kPa

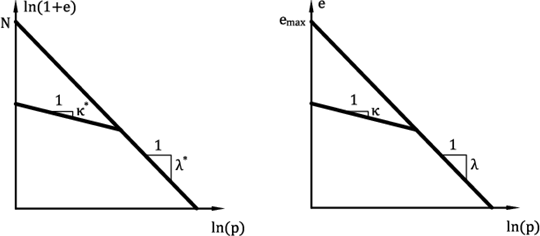Figura 2: Diagrama bilinear de consolidação isotrópica - (a) Argila hipostática, (b) Modelo cam clay

Ângulo de atrito interno crítico φ_cv

• Idêntico para a amostra original (não distribuído) e reconstituída após consolidação consequente
• Pode ser determinado a partir de ensaios triaxias com diferentes aplicações de pressões nas células de uma amostra reconstituída
• Ensaio pode ser realizado em condições drenadas ou não drenadas (mais rápido)
• Os valores mais comuns estão compreendidos entre 18° - 35°

Inclinação da linha de consolidação normal λ*

• É determinada graficamente, a partir do trecho de carregamento do ensaio de edométrico ou de consolidação isotrópica (ver Figura 3)
• Para argilas rígidas, é preferível realizar o ensaio numa amostra reconstituída
• Os valores mais comuns estão compreendidos entre 0.04 - 0.15

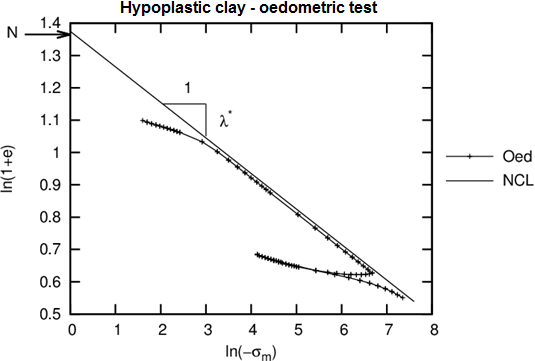Figura 3: Simulação do ensaio edométrico através do modelo hipoplástico

Inclinação da linha de dilatação κ*

• Pode ser determinada graficamente, de forma semelhante à do parâmetro λ*, ou através de um estudo paramétrico - comparando medições de simulações ao longo do trecho de relaxamento de ensaios edométricos ou de consolidação isotrópica (ver Figura 3)
• Os valores mais comuns de κ estão compreendidos entre 0.01 - 0.02
• O rácio λ/κ deve ser superior a 4.0

Origem da linha de consolidação normal N

• É determinada graficamente, a partir do trecho de carregamento de ensaios edométricos ou de consolidação isotrópica
• O ensaio deve ser realizado numa amostra não distribuída - ao procurar a interseção entre a linha lambda com o eixo vertical, é possível determinar a inclinação lambda obtida a partir da amostra reconstituída (ver Figura 3)
• Os valores mais comuns estão compreendidos entre 0.8 - 1.6

Rácio dos módulos unitário e de cisalhamento r

• O significado físico deste parâmetro é dado pela expressão r = K_i/G_i
• K_i corresponde ao módulo tangente unitário da compressão isotrópica, de acordo com a linha de consolidação normal
• G_i corresponde ao módulo tangente de cisalhamento para ensaios de cisalhamento não drenados, assumindo o mesmo estado de tensão
• O parâmetro r pode ser determinado através de um estudo paramétrico do ensaio triaxial de cisalhamento
• Os valores mais comuns estão compreendidos entre 0.05 - 0.7

Definir o estado inicial do solo

Em argilas hipostáticas, o estado do solo depende da sua compactação, representada pelo índice de vazios. A implementação do modelo permite introduzir o volume de vazios inicial, ou atual, diretamente, ou também pode ser calculado a partir da pressão de pré-consolidação introduzida OCR. No primeiro caso, o valor e₀ corresponde ao índice de vazios medido numa amostra sem carregamento, extraída de uma certa profundidade. No segundo caso, o valor e_curr corresponde ao índice de vazios de um solo carregado. Neste último caso, é necessário especificar o valor de OCR. Este parâmetro represente o rácio entre a tensão média em NCL e a tenção média inicial (ver Figura 4b).

Ao iniciar a tarefa recorrendo ao método K_o, é atribuído o estado de tensão atual ao estado de tensão inicial no início da segunda etapa. Se for adotada a análise normal para a primeira etapa (o modelo de argila hipostática é introduzido logo na primeira etapa), em que o solo é carregado pelo seu peso próprio, assume-se o valor da tensão inicial de p_in = 1 kPa e verifica-se e_curr = e₀. Se um material diferente (ex.: um material elástico é considerado para a primeira etapa) for substituído pelo modelo de argila hipostática, adota-se o estado de tensão inicial calculado na etapa anterior. Ao utilizar um material elástica na primeira etapa, o estado de tensão resultante corresponde aos resultados obtidos através do método de método K_o (ν é o coeficiente de Poisson).

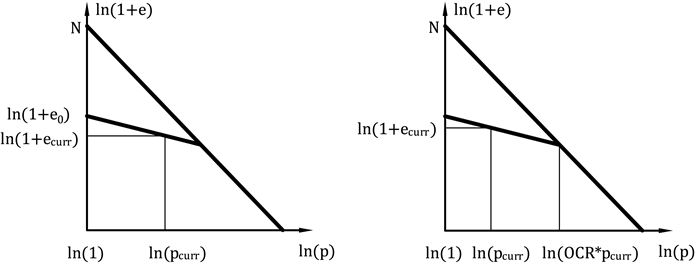Figura 4: Iniciação do índice de vazios - (a) através do índice de vazios inicial, (b) através do OCR

A Figura 5 demonstra que em solos normalmente consolidados, o estado para o qual OCR = 1.0 corresponde apenas a uma consolidação isotrópica, para K_o = 1.0. Se o solo experimentar um estado de tensão de desvio não nulo, o OCR correspondente para um solo normalmente consolidado é superior a 1.0. O valor exato depende dos parâmetros do solo e do percurso da tensão (o valor de K_o). A Figura 5 mostra a relação entre os valores mínimos de K_o e diferentes tipos de solos argilosos. Na Tabela 1 também constam valores particulares. Os parâmetros materiais básicos deste conjunto de solos estão listados na tabela 2.

A escolha de OCR = 1.0 para solos normalmente consolidados com K_o diferente de 1.0, dá origem a estados de tensão não aceitáveis que podem resultar na perda de convergência.

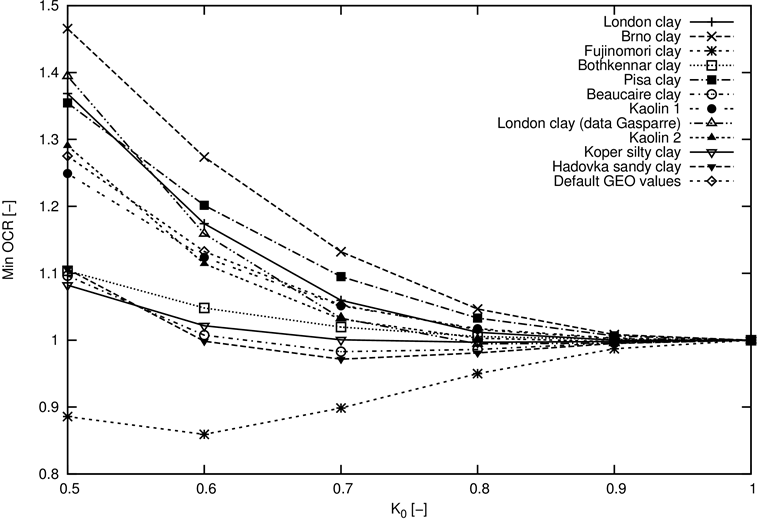Figura 5: Relação entre OCR e o coeficiente do empuxo de terra em repouso K_o

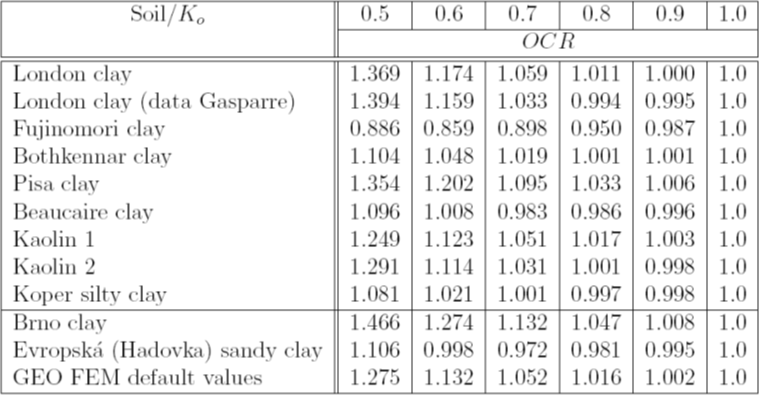Tabela 1: Índice de sobreconsolidação OCR dos solos selecionados em função do valor de K_o

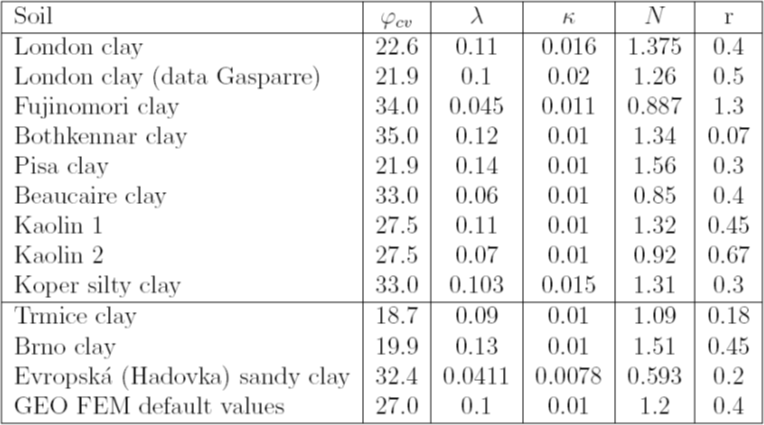Tabela 2: Parâmetros materiais dos solos selecionados

Deformação inter-granular

A versão básica do modelo é adequada para análises com uma direção predominante do carregamento de tensão. Para o caso de carregamentos cíclicos (carregamento-relaxamento-recarregamento), é mais adequado utilizar uma formulação que considere o conceito da deformação inter-granular. Isto permite restringir aumentos de deformações permanentes não aceitáveis, durante pequenas variações de carregamento repetitivas (ratcheting). A introdução de deformações intergranulares permite modelar a rigidez elevada, que as argilas experimentam durante as pequenas deformações. Esta opção não faz parte de nenhum outro modelo implementado no GEO MEF. O conceito das deformações inter-granulares assume que a deformação total do solo consiste numa pequena deformação de uma camada inter-granular (deformação inter-granular) e numa deformação causada pelo deslizamento mútuo das partículas. A alteração do percurso do carregamento, altera a deformação inter-granular. Ao alcançar o valor limite da deformação inter-granular, a deformação associada ao movimento das partículas.

A adoção do conceito de deformações inter-granulares implica a definição de cinco parâmetros adicionais:

• Alcance da deformação inter-granular elástica R
• Parâmetros m_R e m_T de controlo da rigidez de pequenas deformações
• Parâmetros β_r e χ de controlo do nível de degradação da rigidez com o aumento da deformação de cisalhamento

Estes parâmetros são calibrados após conhecer os dados do material do modelo hipoplástico básico.

Margem da deformação inter-granular elástica R

• Determina o alcance da deformação intergranular máxima
• Pode ser determinada através de um estudo paramétrico da curva de degradação G = G(ε_s) (Figura 5)
• Alternativamente, pode ser considerada como uma constante independente do material R = 10^-4
• Os valores mais comuns estão compreendidos entre 2_*10^-5 - 1_*10^-4

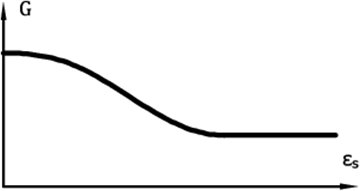Figura 6: Curva que descreve a perda de rigidez do módulo de cisalhamento

Parâmetro m_R

• Determina o valor do módulo de cisalhamento ao variar o percurso do carregamento no plano meridional (σ_m - J) para 180°
• O rácio linear entre o parâmetro m_R e o módulo de cisalhamento inicial G₀ é dado por G₀ = p_*(m_r/(r_* λ*)
• O módulo de cisalhamento inicial pode ser determinado a partir de medições da onda de propagação do cisalhamento [2]
• Os valores mais comuns estão compreendidos entre 4.0 - 20.0

Parâmetro m_T

• Determina o valor do módulo de cisalhamento ao variar o percurso do carregamento no plano meridional (σ_m - J) para 90°
• Verifica-se que m_R/m_T = G₀/G₉₀
• O rácio do módulo inicial pode ser estimado a partir do rácio deste módulo para deformações mais elevadas. Os valores mais comuns do rácio m_R/m_T estão compreendidos entre 1.0 - 2.0
• Os valores mais comuns de m_T estão compreendidos entre 2.0 - 20.0

Parâmetros β_r e χ

• Determina o nível de degradação da rigidez com o aumento da deformação de cisalhamento
• Pode ser determinada através de um estudo paramétrico da curva de degradação G = G(ε_s)
• Os valores mais comuns de β_r estão compreendidos entre 0.05 - 0.5
• Os valores mais comuns de χ estão compreendidos entre 0.5 - 6

Bibliografia:

[1] D. Mašín, A hypoplastic constitutive model for clays, International Journal for Numerical and Analytical Methods in Geomechanics., 29:311-336, 2005.