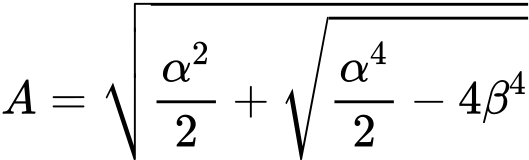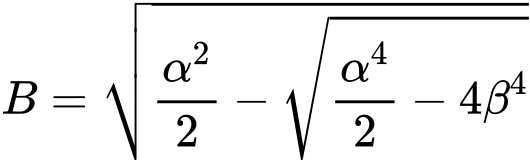Геометрический метод (Эйлера)
Среду, окружающую микросваю, моделируем в программе модулем реакции основания (несущего слоя) Ep (постоянной Винклера k), которую задаёт пользователь в рамке «Проверка сечения». Модель конструкции представлена на рисунке.
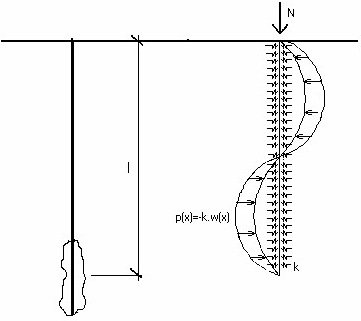 Модель конструкции
Модель конструкции
У сжимаемой микросваи предполагается образование переменного количества полуволн в зависимости от геометрии и жесткости конструкции (среды). Решение в этом случае следует из уравнения изгиба прямого стержня.
![]()
После приведения уравнение изгиба можно представить в следующем виде:
| |
где: | |
| |
| |
| |
|
Для расчёта постоянных интегрирования C1-C4 используем четыре краевые условия, которые выражают способ опирания концов.
Величину критической силы Nc можно вычислить с помощью общего соотношения, известного по теории упругости (см. список литературы [1]):
![]()
где: | Ei | - | модуль упругости идеального поперечного сечения |
Ii | - | момент инерции идеального поперечного сечения | |
lp | - | эффективная длина микросваи (свободная длина микросваи + 1/2 длины корня) | |
Er | - | ||
n | - | количество полуволн линии изгиба вдоль длины микросваи |
Критическую силу Ncr принимаем как минимум функции (1). Он достигается для длины полуволны:
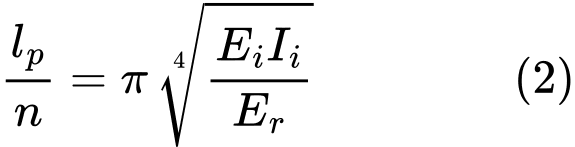
Из уравнения (2) следует отношение для количества полуволн n:
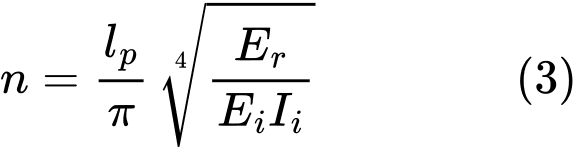
Если часть микросваи расположена над рельефом (смещение головы сваи), то уменьшенные значения n и Er рассчитываем следующим образом:
![]()
![]()
где: | lv | - | длина микросваи над рельефом (грунтом) |
Для расположения микросваи шарнир-шарнир критическую силу Ncr определяем по соотношению:
![]()
Для расположения микросваи шарнир-заделка критическую силу Ncr определяем по соотношению
![]()
Литература:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936