Shahunyants
Metoda Shahunyants jest metodą paskową, opracowaną na bazie równowagi granicznej. Metoda ta wymaga spełnienia równowagi sił i momentów oddziaływujących na poszczególne bloki. Bloki tworzone są poprzez dzielenie gruntu powyżej powierzchni poślizgu, za pomocą płaszczyzn podziałowych. Siły oddziaływujące na poszczególne bloki pokazano na rysunku poniżej:
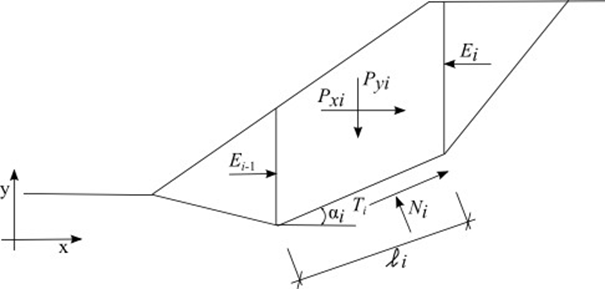Schemat statyczny - metoda Shahunyants
Przyjmuje się, że dla każdego z bloków zastosowanie mają podane poniżej siły:
gdzie: | Pyi | - | wypadkowa sił pionowych oddziałujących na dany blok (ciężar bloku, obciążenie bloku, obciążenie sejsmiczne, siły w kotwach…) |
Pxi | - | wypadkowa sił poziomych oddziałujących na dany blok (obciążenie bloku, obciążenie sejsmiczne, siły w kotwach siły w zbrojeniu…) | |
Ei+1, Ei | - | siły zmobilizowane pomiędzy blokami | |
Ni | - | reakcja pod blokiem normalna do segmentu powierzchni poślizgu | |
Ti | - | siła tarcia na segmencie powierzchni poślizgu | |
αi | - | nachylenie segmentu powierzchni poślizgu | |
li | - | długość segmentu powierzchni poślizgu | |
φi | kąt tarcia wewnętrznego gruntu na segmencie powierzchni poślizgu | ||
ci | spójność gruntu na segmencie powierzchni poślizgu |
W metodzie Shahunyants przyjmowane są podane poniżej założenia, dla wyliczenia równowagi granicznej sił i momentów dla poszczególnych bloków:
- Płaszczyzny podziału między blokami są zawsze pionowe
- nachylenie sił Ei oddziałujących pomiędzy blokami wynosi zawsze zero, siły oddziałują zawsze poziomo
Procedura rozwiązania:
W pierwszej kolejności, siły Pyi oraz Pxi są transformowane z zastosowaniem wyrażeń (1) i (2) do kierunków sił Ti oraz Ni. Dla dodatniego kąta αi (w taki sposób jak na pokazanym schemacie) siła PNi oddziałuje w kierunku przeciwnym do Ni, a siła PQi oddziałuje w kierunku przeciwnym do Ti.
(1)
(2)
Siły oddziałujące wzdłuż segmentu powierzchni poślizgu są powiązane następującą zależnością:
(3)
gdzie: | Ui | - | ciśnienie porowe na segment powierzchni poślizgu |
Dla uzyskania rozwiązania stosuje się następujące równania równowagi dla każdego bloku:
Warunek równowagi w kierunku normalnym do segmentu powierzchni poślizgu:
(4)
Warunek równowagi w kierunku równoległym do segmentu powierzchni poślizgu:
(5)
Wprowadzenie równania (3) do równania (5) daje:
(6)
Następnie, podstawienie równania (4) do równania (6) daje:
(7)
Po przekształceniu:
(8)
Wykorzystując następujące wyrażenie matematyczne:
(9)
doprowadza się równanie 8) do postaci:
(10)
Następnie może być ono zmodyfikowane w sposób następujący:
(11)
w celu otrzymania wyrażenia rekurencyjnego dla sił Ei oddziałujących pomiędzy blokami:
(12)
Na tym etapie analiza dochodzi do współczynnika bezpieczeństwa Ku. Współczynnik bezpieczeństwa jest wartością, która sprowadza siły oddziałujące na poszczególne bloki gruntu do stanu stanów granicznych. Stan taki można osiągnąć przemnażając siły aktywne, tj. siły powodujące przesunięcie masywu gruntowego po powierzchni poślizgu. W równaniu (12) siły aktywne są zawarte w określeniu PQi. Wyrażanie to zawiera jednocześnie siły aktywne powodujące przesuw oraz siły utrzymujące - przeciwstawiające się przesunięciu. Siły przesuwające będą opisane jako PQi,sd a siły utrzymujące jako PQi,ud. Równanie (12) przybiera wówczas postać:
(13)
Jeśli wartość PQi jest dodatnia wówczas przyczynia się do powstania przesunięcia i bedzie przyjmowana jako siła aktywna PQi,sd. Jeśli wartość PQi jest ujemna, czyli przeciwstawia się przesunięciu będzie przyjmowana jako siła PQi,ud. Dlatego odejmowanie wartości PQi,ud, która jest ujemna, w równaniu (13) oznacza dodanie wartości dodatniej, wobec czego można zapisać:
(14)
Na początku powierzchni poślizgu E0 = 0. Wartość E1 opisana jest równaniem:
(15)
Wartość E2 natomiast można przedstawić następująco:
(16)
Podobnie można wyznaczyć wartości wszystkich sił oddziałujących pomiędzy blokami. Ponadto w punkcie końcowym powierzchni poślizgu En = 0. Wykorzystując wcześniejsze zależności można zapisać:
(17)
Powyższe równanie pozwala bezpośrednio podaje współczynnik stateczności Ku jako:
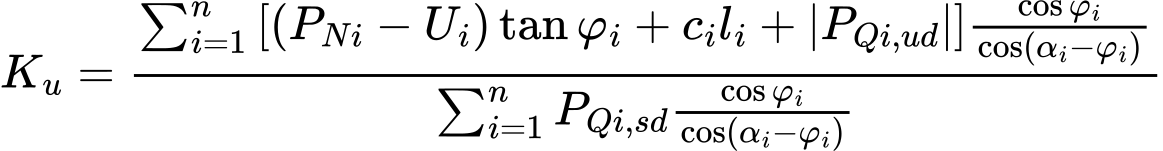(18)