Empuxo Ativo - Teoria de Mazindrani (Rankine)
O empuxo ativo é dado pela seguinte expressão:
![]()
onde: | σz | - | tensão vertical geostática |
Ka | - | coeficiente de empuxo ativo segundo Rankine | |
β | - | inclinação do talude | |
γ | - | peso do solo | |
z | - | profundidade | |
| - | coeficiente de empuxo ativo segundo Mazindrani |
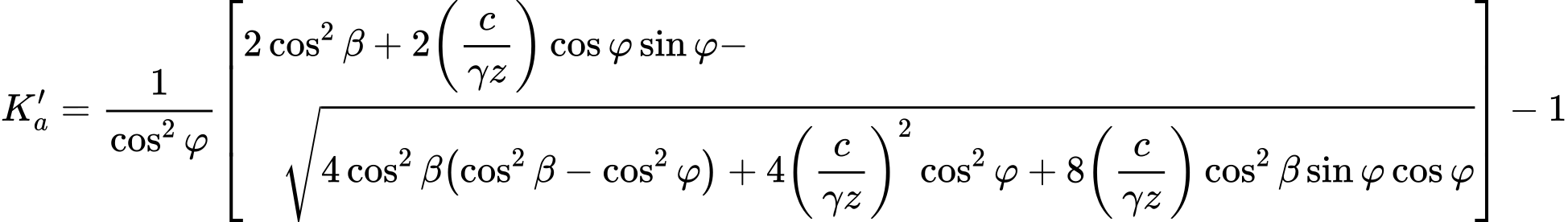
onde: | β | - | inclinação do talude |
φ | - | ângulo de atrito interno do solo | |
c | - | coesão do solo |
Para solos não coesivos (c = 0) com superfície do terreno horizontal (β = 0) o empuxo ativo é obtido através da solução de Rankine:
![]()
sendo o coeficiente de empuxo ativo:
![]()
onde: | φ | - | ângulo de atrito interno do solo |
As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()
onde: | σa | - | empuxo ativo |
δ | - | ||
α | - | inclinação da parede da estrutura |
Bibliografia:
Mazindrani, Z.H., and Ganjali, M.H. 1997. Lateral earth pressure problem of cohesive backfill with inclined surface. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 123(2): 110-112.